Fraunhofer-Institut für Techno- und Wirtschaftsmathematik ITWM
Fraunhofer-Institut für Techno- und Wirtschaftsmathematik ITWM
Filter Fasern
© fotalia / Fraunhofer ITWM
Filter Fasern

© fotalia / Fraunhofer ITWM

Modellierung von Mikrostrukturen: Fasersysteme

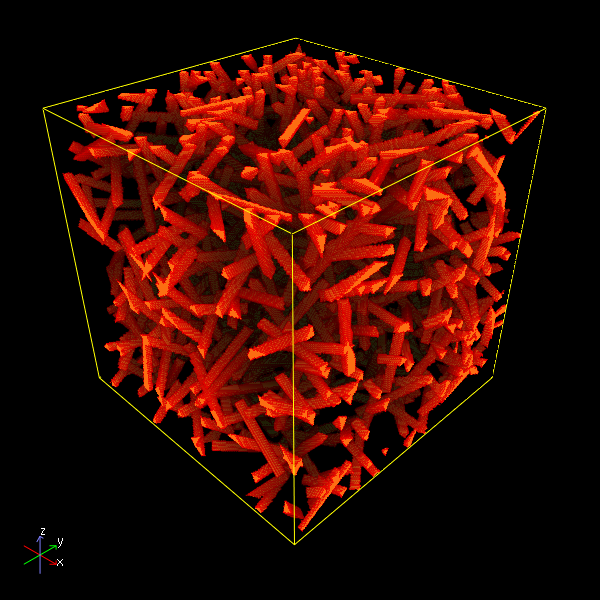
Stochastische Geometriemodelle werden anhand geometrischer Charakteristiken, die in 3D Bilddaten gemessen werden, an reale Strukturen angepasst. Durch Änderungen der Modellparameter ergeben sich daraus virtuelle Fasersysteme mit verschiedenen Mikrostrukturen. Die Auswirkungen auf die makroskopischen Eigenschaften dieser Fasersysteme können dann mittels numerischer Simulationen untersucht werden.

Boolsche-Modelle und Poisson-Prozesse sind weitverbreitete Modelle für Faserstrukturen. Für beide Modelle kann die Orientierungsverteilung der Zylinder so gewählt werden, dass sie mit der beobachteten Verteilung im Material übereinstimmt – isotrop und anisotrop, zum Beispiel, wenn die Zylinderachsen in zueinander parallelen Ebenen liegen oder sie in einer bevorzugten Richtung angeordnet sind.

Boolean Model

Dilatiertes Poissonsches Geradenfeld
© Fraunhofer ITWM
Dilatiertes Poissonsches Geradenfeld, Orientierungen in z-Richtung bevorzugt
Boolsches Modell trilobaler Zylinder
© Fraunhofer ITWM
Boolsches Modell trilobaler Zylinder, isotrop
Boolsches Modell trilobaler Zylinder
© Fraunhofer ITWM
Boolsches Modell trilobaler Zylinder, Orientierungen in x-y-Ebene bevorzugt

Die Modellierung dichter Systemen nicht überlappender gekrümmter Fasern erfordert ein anderes Modell. Das Altendorf-Jeulin-Modell entsteht in zwei Schritten:

  1. Zuerst werden mit einer zufälligen Irrfahrt mit multivariater von Mises-Fisher-Orientierungsverteilung gekrümmte Fasern erzeugt.
  2. Danach ordnet ein Packungslagorithmus abgeleitet vom Force-Biased-Algorithmus die Fasern nicht überlappend an.

Alle Parameter, die für die Anpassung an die reale Mikrostruktur benötigt werden, können aus 3D-Bildern gewonnen werden. Bei einem Verhältnis von Faserlänge zu Faserdicke bis 15 können isotrope Faserssysteme mit Faservolumenanteilen über 60 Prozent generiert werden.

Altendorf-Jeulin Model

Z-Richtung bevorzugt
© Fraunhofer ITWM
Z-Richtung bevorzugt
Isotropie
© Fraunhofer ITWM
Isotropie
Isotropie in der x-y-Ebene
© Fraunhofer ITWM
Isotropie in der x-y-Ebene

Das von Hellen Altendorf entwickelte stochastische Modell generiert Fasersysteme mit einzelnen Fasern. Da z.B. Vliese oft auch Faserbündel enthalten, wird das Altendorf-Jeulin-Modell dahingehend verallgemeinert, dass Faser-Faser-Interaktionen möglich werden. Realisierungen des Modells mit Faserbündeln sind in der Abbildung unten zu sehen.

Easwaran-Altendorf-Jeulin Model

Z-Richtung bevorzugt
© Fraunhofer ITWM
Z-Richtung bevorzugt
Isotropie
© Fraunhofer ITWM
Isotropie
Isotropie in der x-y-Ebene
© Fraunhofer ITWM
Isotropie in der x-y-Ebene

Veröffentlichungen

  • P. Easwaran, P.; Lehmann, M. J.; Wirjadi, O.; Prill, T.; Didas, S.; Redenbach, C.:
    Automatic Fiber Thickness Measurement in SEM Images Validated Using Synthetic Data.
    Proceedings of FILTECH 2015.
    Filtech Exhibitions Germany: Cologne.
  • Redenbach, C.; Schladitz, K.; Vecchio, I.; Wirjadi, O. :
    Image Analysis for Microstructures Based on Stochastic Models.
    GAMM-Mitteilungen. 37, (2), 281-305, (2014).
  • Altendorf H.; Jeulin D.: 
    Random-walk-based stochastic modeling of three-dimensional fiber systems.
    Phys. Rev. E 83, 041804, 2011.

Das könnte Sie auch interessieren: