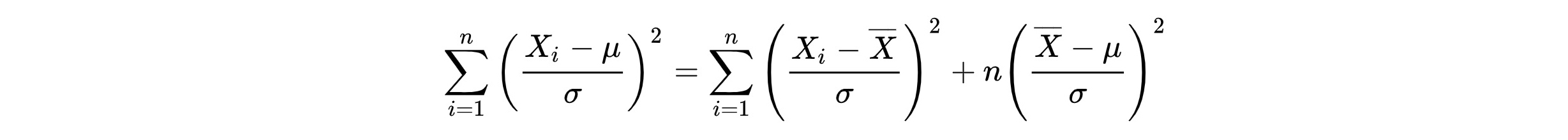Unser Kollege Sascha Feth über Schützen mit zitternden Händen oder einem Knick in der Optik und eiförmige Zielscheiben. Wo da ein Zusammenhang besteht und was das auch noch mit Statistik zu tun hat – hier im neuen Blog-Post.
© iStockphoto
In der Formel für die Standardabweichung taucht ein ominöses »N-1« auf, das Studierende regelmäßig in den Wahnsinn treibt: "Wieso minus 1?" Wir erklären Euch dieses Mysterium anhand des Fallbeispiels eines Schützen, der zitternde Hände oder einen Knick in der Optik hat.
Die ersten Stunden jedes Einstiegskurses in Statistik für Mathe-Studierende werden oft genutzt, um die Formeln für den (arithmetischen) Mittelwert und die (Stichproben-)Standardabweichung zu bewundern:
Vermutlich beten dann die meisten Dozierenden: »Bitte, lass niemanden nachfragen, warum man beim Mittelwert durch die Anzahl der Beobachtungen dividiert, man bei der Standardabweichung das mittlere Fehlerquadrat aber mit einer zu niedrigen Zahl, nämlich N-1 dividiert.« Es ist nämlich schwierig, dann nicht herumzudrucksen. Hier nun ein Entzauberungsversuch:
Spoiler: Es hat nichts damit zu tun, dass man durch das N-1 nicht versuchen kann, aus nur einem Wert eine Varianz zu bestimmen.
| Bitte beachten Sie, dass man für die Berechnung der Standardabweichung den arithmetischen Mittelwert verwendet. Viel lieber würde man natürlich den unbekannten wahren Mittelwert verwenden, doch den kennt man ja nicht. Das wird später noch relevant. |
Wir stellen uns nun vor, dass wir Leute an der Schießbude eines Jahrmarktes beobachten.
Welchen der beiden Schützen A und B würden Sie zum besseren Schützen küren? Vermutlich wählen Sie Schütze A. Welchen Tipp würden wir den beiden Schützen geben? A sollte ermuntert werden viel zu üben, um eine ruhige Hand zu bekommen. B hingegen könnte schlagartig besser werden, wenn wir ihm folgendes sagen: »Ziele zuerst so wie du es gewohnt bist, bewege dann den Lauf aber einen Millimeter nach rechts und dann nach unten bevor du abdrückst«. Damit könnten wir ihn (fast) zu einem Meisterschützen machen.
Nehmen wir als Beispiel die Verteilung des Intelligenzquotienten. Der durchschnittliche IQ des Menschen, also der Mittelwert ist 100 und die Standardabweichung hat einen Wert von 15 (Quelle). Dahinter steckt natürlich selbst wieder eine Statistik mit einer (hoffentlich) großen Stichprobe. Für unsere Zwecke nehmen wir kurz an, das sei die unumstößliche Wahrheit: Der wahre Mittelwert ist 100 (dann nennt man ihn Erwartungswert) und die wahre Standardabweichung ist 15.
Und nun vergessen wir diese Wahrheit für einen Moment direkt wieder. Wie könnten wir herausfinden, wo Mittelwert und Standardabweichung liegen? Mit Stichproben natürlich. Also suchen wir uns zufällig 10 Personen an einem möglichst repräsentativen Ort und lassen sie einen IQ-Test absolvieren. Daraus berechnen wir Mittelwert und Standardabweichung. Das könnte z.B. unser Resultat sein:
Wir haben für die zehn Personen einen Mittelwert von ca. 97,83 (also ein bisschen zu wenig) und eine Standardabweichung von 16,90 (also ein bisschen zu viel) berechnet. Das können wir als Schützen interpretieren: Einmal hat der Mittelwertschütze geschossen und die 97,83 getroffen, einmal hat der Standardabweichungsschütze getroffen und die 16,90 getroffen:
Die Zielscheibe ist hier der Zahlenstrahl und wo die »Mitte der Zielscheibe« war, haben wir kurz vergessen (es war 100 bzw. 15). So ein Schuss ist damit ziemlich aufwändig! Wir mussten zehn Personen suchen, testen und dann die klassischen Formeln anwenden.
| In der Realität ist das Unsinn. Hätten Sie Geld und Zeit für 20 Probanden gehabt, hätten Sie direkt 20 Probanden getestet und nicht zweimal das gleiche Experiment gemacht, um zu sehen wie sich Mittelwert und Standardabweichung unterschiedlich ergeben. Hier im Gedankenexperiment leisten wir uns diese Narretei. |
Wenn wir schon dabei sind, wiederholen wir das nicht nur einmal sondern dutzende, hunderte Male. Dank Zufallszahlengenerator in Excel ist das kein Problem. Das hier haben die Schützen nach 1.000 Schuss abgeliefert:
Viel sieht man in dieser Darstellung nicht. Die Schüsse tummeln sich irgendwie schon um die wahren Werte bei 100 und 15, streuen aber auch recht stark. Zunächst bescheinigen wir beiden Schützen eine zittrige Hand. Haben die beiden auch einen Knick in der Optik? Dazu müssen wir uns eine Meta-Ebene höher ansiedeln und den Mittelwert der 1.000 Mittelwerte und Standardabweichungen rechnen:
Dass die Abweichung bei der Standardabweichung systematisch ist, müssen Sie mir im Moment glauben. Somit hat nur der Standardabweichungsschütze einen Knick in der Optik.
Die Formel der (Stichproben-)Standardabweichung ist eine Variante der Formel für die (Stichproben-)Varianz:
(so nennen Statistiker die Standardabweichung, bevor die Wurzel daraus gezogen wurde). Die wahre Varianz liegt bei 152 = 225. Nun kommt ein Varianzschütze dazu, der uns im Mittel 224,61 geliefert hat (dazu muss man die Werte des Standardabweichungsschützen einzeln quadrieren und dann eben wieder den Mittelwert bestimmen). Diese leichte Differenz wird wieder komplett verschwinden, wenn wir den Simulationsumfang anheben.
Würden Varianzen mit N statt N-1 berechnet, so würde der Varianzschütze mit ca. 202 deutlich nach unten von der wahren 225 abweichen. Das haben die Statistiker bereits früh erkannt und konnten analytisch argumentieren, dass der Varianzschützen seinen Knick in der Optik verliert, wenn man ihn mit N-1 arbeiten lässt.
Schaut man sich das analytische Argument genauer an, begegnet einem die Chi-Quadrat-Verteilung. Würde man für die Berechnung der Varianz den wahren Mittelwert – sprich Erwartungswert – verwenden, hätte diese N Freiheitsgrade und alles wäre gut. Nun kennt der Varianzschütze diesen aber nicht. Neben ihm steht noch der Mittelwertschütze, der ihm sein eigenes Einschussloch als Annäherung für den Erwartungswert nennt. Das erschwert unserem Varianzschützen die Arbeit unnötig. Die Freiheitsgrade der Chi-Quadrat-Verteilung verändern sich jetzt auf N-1.
Es ist schwierig, das nun griffig zu interpretieren. Dazu braucht man den Satz von Cochran. Die kritische Formelzeile ist hierbei diese:
Links steht unsere Wunsch-Formel für die Varianz (mit dem unbekannten Erwartungswert) mit N Freiheitsgraden. Rechts eine Summe aus unserer Ist-Formel (geschätzter Mittelwert) und etwas mit einem Freiheitsgrad. Also bleiben N-1 Freiheitsgrade für unsere Ist-Formel. Exkurs Ende.
Kommt Ihnen daran nicht etwas seltsam vor? Der Varianzschütze trifft im Mittel ins Schwarze (d.h. die 225), wenn er N-1 benutzt. Der Standardabweichungsschütze (der sich nur durchs Wurzelziehen unterscheidet) trifft nun plötzlich nicht mitten ins Schwarze (bei ihm 15).
Hier hinkt unser Vergleich ein wenig. Das wäre so, als würde ein Schütze, der bei eiförmigen Zielscheiben eine hervorragende Leistung zeigt, plötzlich bei kreisrunden Zielscheiben versagen. Schaut man als Mathematiker darauf, wundert man sich nicht, denn die Wurzeltransformation ist nicht linear:
Alle Formeln, die uns bisher begegnet sind, bestechen durch ihr riesiges Summenzeichen. Und denen ist es eben nicht egal, ob da nun noch eine Wurzel gezogen wird oder nicht.
Mittelwerte weichen nicht systematisch vom wahren Mittelwert (Erwartungswert) ab. Varianzen auch nicht, sofern man N-1 benutzt. Standardabweichungen leider dann doch wieder, trotz N-1.
Für den Moment können wir es dabei belassen. Schließlich ging es uns darum, dem N-1 ein bisschen auf die Spur zu kommen. An zwei Stellen drängen sich noch Fragen auf:
Die Antworten folgen demnächst in einem eigenen Beitrag.
Wie genau lässt sich eigentlich eine Streuung aus Daten ermitteln? Oder anders gefragt: Was ist die Streuung der Streuung?
Und welche Rolle spielen dabei die ominösen t- und Chi-Quadrat-Verteilungen? In diesem Beitrag gehen wir der Sache auf den Grund.
Fraunhofer-Institut für Techno- und Wirtschaftsmathematik ITWM