Fraunhofer Institute for Industrial Mathematics ITWM
Fraunhofer Institute for Industrial Mathematics ITWM
Filling a beer glass simulated with MESHFREE
© iStockphoto/Fraunhofer ITWM
Filling a beer glass simulated with MESHFREE - foaming in particular plays a major role in this process.

Process Simulation for the Food Industry

Among others MESHFREE simulates a variety of food technology processes including the foam filling process in a beer glass.

© iStockphoto/Fraunhofer ITWM

In fluid dynamics, a Kármán vortex street is a repeating pattern of swirling vortices in a flow around an obstacle.
© Fraunhofer ITWM
In fluid dynamics, a Kármán vortex street is a repeating pattern of swirling vortices in a flow around an obstacle.

Going into detail

In fluid dynamics, a Kármán vortex street is a repeating pattern of swirling vortices in a flow around an obstacle. Flexible refinement strategies in MESHFREE enable fast calculation times to be combined with attention to detail.

© Fraunhofer ITWM

Simulations with MESHFREE

MESHFREE is an innovative software tool in fluid and continuum mechanics developed in cooperation with Fraunhofer SCAI. It combines the expertise in meshfree simulations and scientific computations of the two institutes.

 

Universal Model for Fluids and Solids

MESHFREE uses a general material model, which allows to simulate complex materials (non-Newtonian fluids, foams or viscoelastic materials) with the same numerical method. The medium does not need to be declared as fluid or solid a priori to choose an appropriate numerical solver. Instead, only material properties such as viscosity or shear modulus are required to predict the material behavior.

 

Faster Results with MESHFREE

The software MESHFREE combines the Finite Pointset Method (FPM) for solving the conservation equations of mass, momentum and energy with efficient algorithms for solving linear systems of equations. The underlying method is based on a cloud of numerical points without explicit neighborhood information of a mesh, so the need for costly meshing and re-meshing disappears.

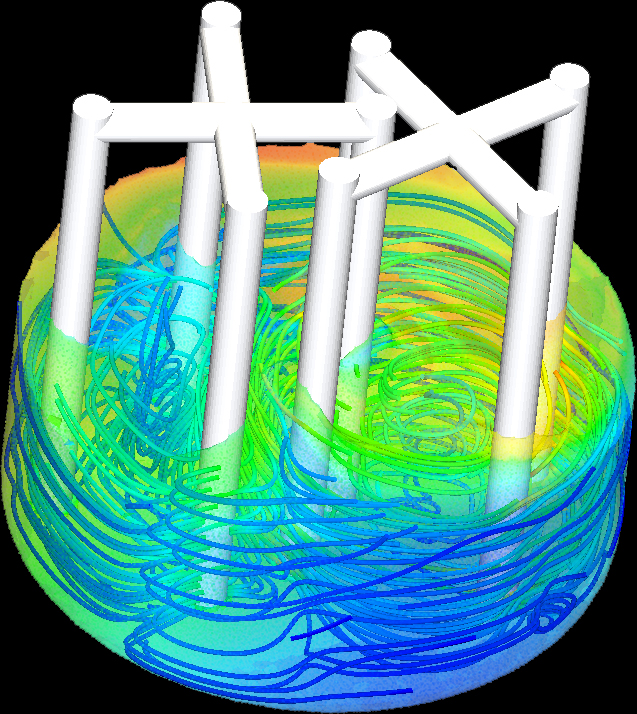
The geometry can be exported directly from CAD tools and used for the simulation. Due to the complete absence of a volume mesh, MESHFREE is highly flexible regarding the discretisation of the computational domain in highly dynamic processes, such as flows with free surfaces or fast moving geometry elements.

Der Benutzer exportiert direkt die Geometrie aus gängigen CAD Tools und verwendet sie für die Simulation. Durch das Fehlen eines Rechengitters ist MESHFREE enorm flexibel in der Organisation der Rechenpunkte; denn es entsteht kein aufwändiges Anpassen der Netztopologie bei hochdynamischen Prozessen – wie beispielsweise bei Strömungen mit freien Oberflächen oder sich schnell bewegenden Geometrieelementen. 

© Fraunhofer ITWM

Eine Simulation eines Rührprozesses mit MESHFREE.

 

Der Benutzer exportiert direkt die Geometrie aus gängigen CAD Tools und verwendet sie für die Simulation. Durch das Fehlen eines Rechengitters ist MESHFREE enorm flexibel in der Organisation der Rechenpunkte; denn es entsteht kein aufwändiges Anpassen der Netztopologie bei hochdynamischen Prozessen – wie beispielsweise bei Strömungen mit freien Oberflächen oder sich schnell bewegenden Geometrieelementen. 

Together with VW, we simulate rollover processes on sandy surfaces.
© Volkswagen AG
Together with automobile manufacturer VW we rely on VPS (Virtual Performance Solution), a software package from the ESI Group, to simulate rollover processes on sandy surfaces.
Simulation of a stirring process with MESHFREE.
© Fraunhofer ITWM
Simulation of a stirring process with MESHFREE.

MESHFREE adapts efficiently to moving geometry elements such as stirrers of mixing devices or the movement of free surfaces. Hence, MESHFREE simulations can cover a wide range of applications.

The software tool can be used in many areas, including

  • water management in the automotive industry,
  • flow of rain water,
  • formation of foam,
  • deep drawing and pressing processes,
  • sophisticated fluid-structure interactions,
  • dynamics of granular media like sand, gravel, snow, grain, flour, etc.

We are significantly expanding the focus of meshfree simulation. Not only do we rely on completely new applications, for example, for process engineering or processes in the food industry. We are also exploring a much wider range of materials. In addition to traditional computational fluid dynamics (CFD), we also focus on non-Newtonian fluids – for example, foams, batters, or polymer melts.

 

Synthesis of Successful Softwares

With MESHFREE, the user benefits from extensive experience and expertise of the two Fraunhofer institutes ITWM and SCAI in simulations of complex physical processes. The product is a synthesis of two software tools (FPM and SAMG) that have been successfully applied in many different industry sectors independently for over 15 years and are both being continuously developed.

Video: Simulation Tool MESHFREE »Getting to the Points«

Steffen Hagmann from Porsche, one of the project partners, explains how they use the software in vehicle development. Our expert Isabel Michel and expert Jörg Kuhnert explain in which other areas MESHFREE is used.

Privacy warning

With the click on the play button an external video from www.youtube.com is loaded and started. Your data is possible transferred and stored to third party. Do not start the video if you disagree. Find more about the youtube privacy statement under the following link: https://policies.google.com/privacy

Example Project

 

© iStockphoto

Extrusion Simulation of Bicomponent Synthetic Fibers

In the BiGOFil project, we are working with our partners to increase the efficiency of oil-separating gas filters.

More
 

© Fraunhofer ITWM

SimuSTART – Easy Access to Numerical Simulations

We develop a solution tailored to SMEs that will facilitate entry into MESHFREE and the world of grid-free simulation.

More

Related Links: