GaspiLS – Scalable Software Solution for CFD and FEM Simulations

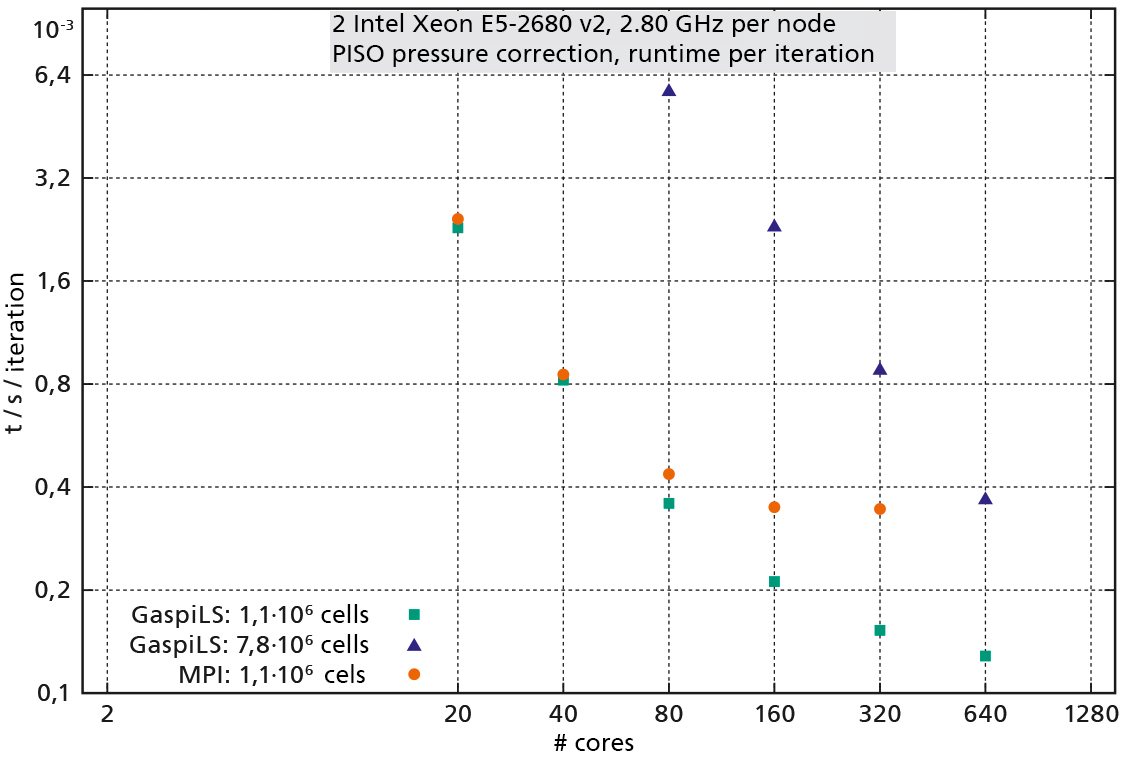
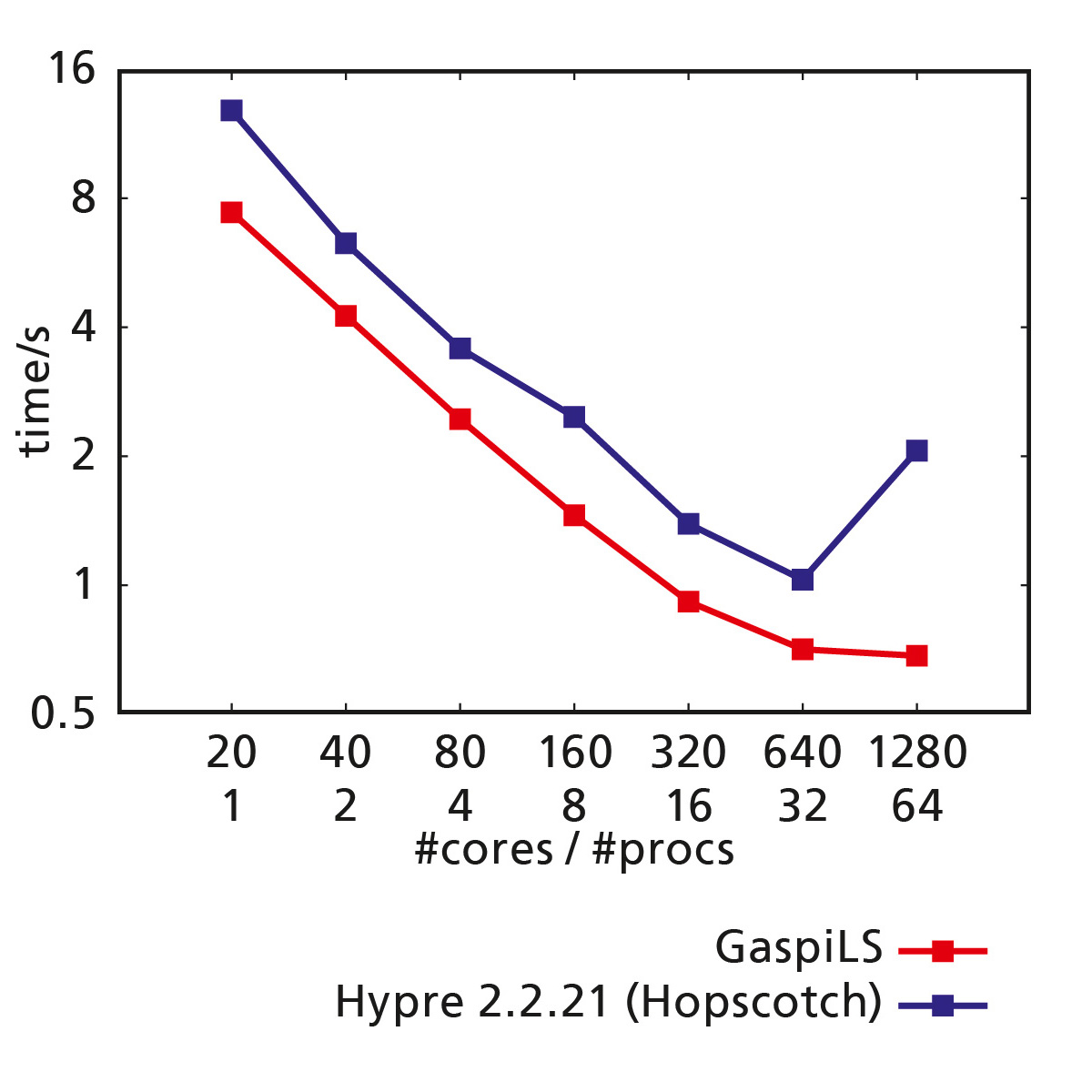
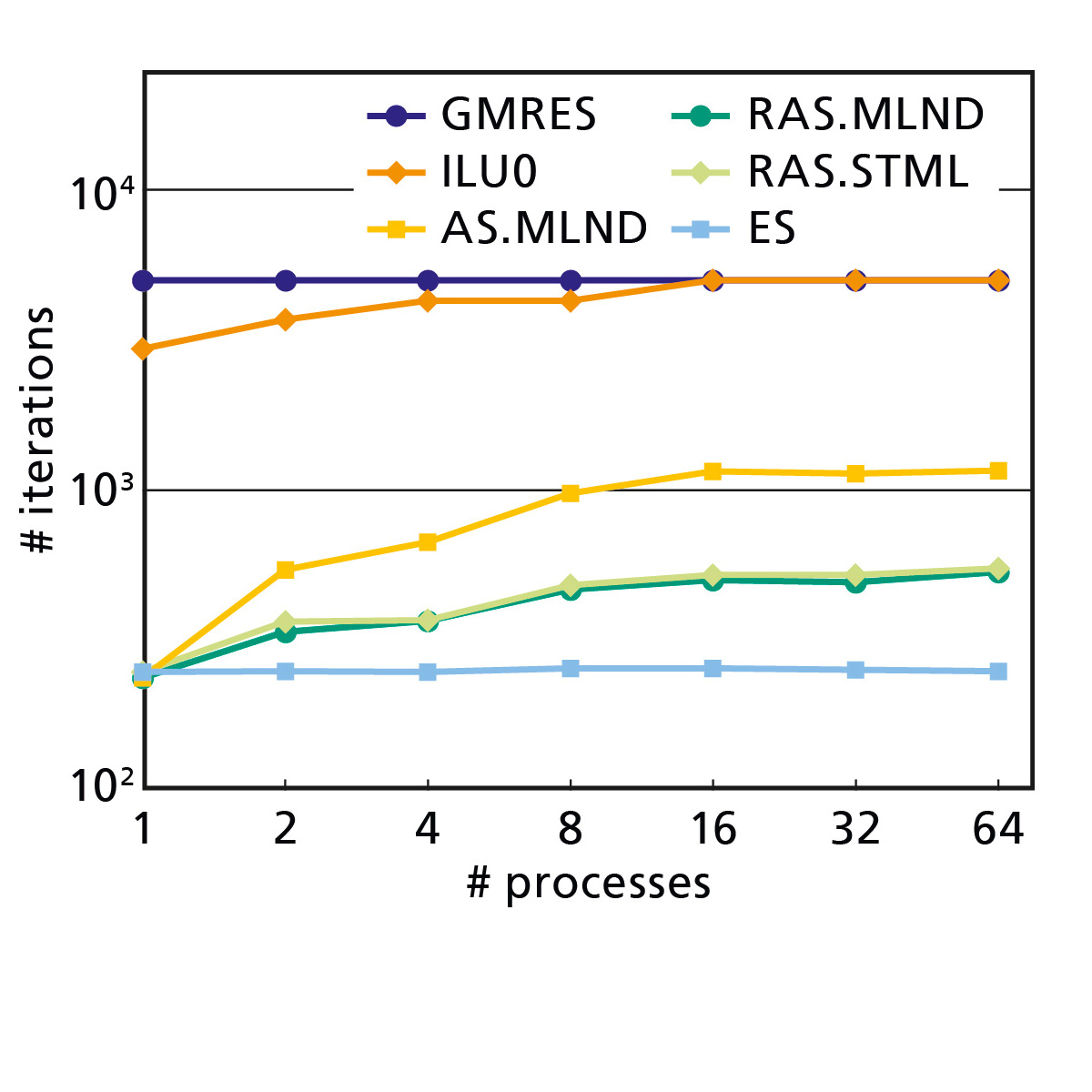
GaspiLS is our scalable linear solver library, which has already proven itself in industrial companies in times of exascale computing. Many simulations in engineering are based on Computational Fluid Dynamics and Finite Element Methods (CFD and FEM methods), for example the determination of aerodynamic properties of aircraft or the analysis of building statics. A large part of the computational time is required for solving the underlying equations by iterative methods such as the Krylov Subspace. The performance of the iterative solvers used thus has a large impact on the overall runtime of such simulations. To gain faster insights from these simulations, we have developed the linear solver library GaspiLS.
 

Industry Relies on Gaspils Due to Better Scalability

Scalability is considered a measure of parallel efficiency in an implementation. The optimum is the so-called linear scalability. This corresponds to the full utilization of computing resources, i.e. the cores within one or more CPUs connected via a network. Improved scalability enables more computing capacity to be used profitably.

In implementation, the following advantages result:

• more detailed models
• more accurate parameter studies
• cost-efficient utilization of hardware resources

We do this without global synchronization points and, in combination with the large amount of generated subproblems, compensate for inequalities in computation time and latency caused by the exchange of data. Each individual core is maximally utilized at all times.
 

Optimal Convergence for a Wide Range of Problems

Preconditioners are designed to improve the convergence of iterative Krylov subspace methods. They reduce the number of required iterations or even enable the solution of a given problem in the first place. Preconditioners are therefore an equally central component for GaspiLS, along with the underlying high-performance matrix vector multiplication, to efficiently solve sparse linear systems of equations.

GaspiLS now provides two different classes of black-box preconditioners:

1. An Algebraic Multigrid Method (AMG) for symmetric positive definite problems, such as those encountered in CFD applications.
2. A multi-level incomplete LU decomposition (Multi-Level ILU) in combination with different domain decomposition methods for general problems.

Both implementations use a scalable, efficient, and hybrid parallel Gaspi-based programming model.

AMG, as a multigrid method, has linear numerical complexity, i.e., the effort to solve increases only proportionally to the number of unknowns to be solved. This is optimal and is used for symmetric positive definite problems. A hierarchy of operators is constructed directly from the matrix without requiring explicit knowledge of the underlying geometry or the partial differential equation.

Multilevel ILU are robust, accurate and, as black-box preconditioners, optimally suited for general sparse systems of equations. ILU essentially consists of a Gaussian elimination procedure in which less important contributions are discarded. Depending on the parameters used and the resources available, our multi-level ILU implementation can interpolate between a full Gaussian elimination (exact inverse, high resource requirement) and a simple Jacobi preconditioner (low resource requirement, low approximation accuracy). In combination with different overlapping or non-overlapping domain decomposition methods available for parallelization, our implementation provides a comprehensive arsenal of methods to implement different preconditioners optimized for the problem at hand. Thus, even poorly conditioned problems can be solved in an optimal way.